Herr Leibniz und sein Dualzahlenrechner

Gottfried Wilhelm Leibniz, den wir im laufenden Jahr feiern, gehört auch zu den Urvätern der Informatik. Er beschrieb das Rechnen im Dualsystem und ein Gerät, das mit den Ziffern 0 und 1 multipliziert. Sein Konzept wurde 1972 und 2005 in zwei Funktionsmodellen umgesetzt. Schon 1931 erfand der Franzose Raymond Valtat eine Rechenmaschine für das Dualsystem.

Der liebe Gott gab uns zehn Finger, und wir sind ganz glücklich mit dem Dezimalsystem, in dem wir addieren, subtrahieren, multiplizieren und dividieren können. Doch schon 1703 brachte die Zeitschrift der Königlichen Akademie der Wissenschaften zu Paris eine Explication de l‘arithmetique binaire, mit anderen Worten, des Rechnens allein mit den Ziffern 0 und 1.

Autor war der Universalgelehrte Gottfried Wilhelm Leibniz. Unter seinen Akten in Hannover lag ein weiterer Text zum Thema. De Progressione Dyadica hatte er am 15. März 1679 verfasst, als er 32 Jahre alt war. Das drei Seiten lange lateinische Manuskript erläutert das Rechnen im Dualsystem und skizziert auch schon einen Apparat zur Multiplikation von Dualzahlen. Der Text wurde 1966 von der Siemens AG als „Herrn von Leibniz‘ Rechnung mit Null und Eins“ auf Deutsch herausgebracht.

Wie sieht jener Apparat aus? Dazu heißt es im Buch: „Eine Büchse soll so mit Löchern versehen sein, dass diese geöffnet und geschlossen werden können. Sie sei offen an den Stellen, die jeweils 1 entsprechen, und bleibe geschlossen an denen, die 0 entsprechen. Durch die offenen Stellen lasse sie kleine Würfel oder Kugeln in Rinnen fallen, durch die anderen nichts. Sie werde so bewegt und von Spalte zu Spalte verschoben, wie die Multiplikation es erfordert.“ Die Spalten meinen natürlich die übereinander stehenden Ziffern, die wir aus dem schriftlichen Multiplizieren kennen.

Und weiter im Text: „Die Rinnen sollen die Spalten darstellen, und kein Kügelchen soll aus einer Rinne in eine andere gelangen können, es sei denn, nachdem die Maschine in Bewegung gesetzt ist. Dann fließen alle Kügelchen in die nächste Rinne, wobei immer eines weggenommen wird, welches in ein leeres Loch fällt, sofern es allein die Tür passieren will. Denn die Sache kann so eingerichtet werden, dass notwendig immer zwei zusammen herauskommen, sonst sollen sie nicht herauskommen.”

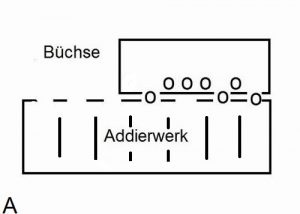
Der Apparat besteht demnach aus einer Büchse mit Kugeln, die man – vielleicht auf einer schiefen Ebene – neben einem Kasten mit Rinnen verschiebt. Die Büchse hat eine Reihe verschließbarer Löcher; ein offenes steht für die Ziffer 1, ein geschlossenes für die 0. In Bild A lassen das linke und die zwei rechten Löcher Kugeln durch, sie ist also auf die Dualzahl 1011 bzw. Dezimalzahl 11 eingestellt. Dabei möge bei einer bestimmten Position der Büchse durch jede Öffnung genau eine Kugel rollen.

Der Kasten neben der Büchse hat auf der Oberseite ebenfalls eine Lochreihe – im Bild sind es sieben Stück. Es ist klar, dass die Büchse an vier Positionen stoppen kann, um Kugeln zu entlassen. Eine hineingerollte Kugeln lässt sich dann als 1 deuten, ein leerer Platz als 0. Die drei Kugeln von Zeichnung A schreiben also 1011 in den Kasten ein. Würde man die Büchse vor Freigabe der Kugeln eine Position nach links verschieben, so würden sie zur Zahl 10110 führen. Ein Vorschub um zwei oder drei Stellen liefert analog 101100 bzw. 1011000.

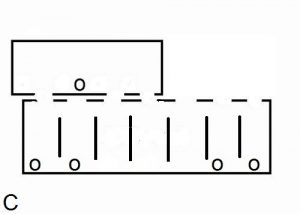
Nun rechnen wir einmal 1011 x 1001 aus. Die 1011 entspricht den offenen Löchern unserer Büchse, die 1001 bedeutet, dass an den Positionen ganz links und ganz rechts Kugeln herausrollen. Am Ende liegen, wie Bild B zeigt, sechs Stück im Kasten. Das Ganze entspricht der Addition 1011 + 1011000, allerdings noch ohne Übertrag. Das Kugelpaar in der Mitte muss verschwinden und links von ihm eine Kugel hinzukommen. Weil dort schon eine Kugel liegt, gibt es den nächsten Übertrag, dann aber sind wir fertig: 1011 x 1001 = 1100011 oder dezimal 11 x 9 = 99. Den Endzustand zeigt Bild C.

Zur Technik des Übertrags sagte Leibniz wenig, es findet sich nur eine durchgestrichene Notiz von „einer kleinen Maschine mit zweizähnigen Rädern“. In dem Addierwerk des Geräts muss aber etwas mit den Kugeln passieren, die aus der Büchse kullern. 1972 baute der Wissenschaftshistoriker Ludolf von Mackensen im Deutschen Museum München einen funktionsfähigen Rechner, der das Leibnizsche Konzept realisierte. Eine Kopie entstand 1985 in Kassel. 2004 konstruierte der Feinmechaniker Gerhard Weber ein neues Modell, das in der Leibniz-Ausstellung der Universität Hannover steht.

Ein besserer Weg könnte ein Murmeladdierer sein. Dieser besitzt eine geniale Übertragsmechanik, die im Eingangsbild zu erkennen ist. Jede Wippe zeigt hier eine Binärzahl an: Eine Neigung nach links bedeutet 0, ist die rechte Seite unten, haben wir eine 1. Im ersten Fall wird eine Murmel, die von oben kommt, nach rechts abgelenkt und die Wippe umgestellt. Im zweiten Fall stellt die Murmel die Wippe ebenfalls um, rollt aber nach links zur nächsten Wippe. Am schnellsten versteht man das durch ein Video des Erfinders, des Deutschkanadiers Matthias Wandel.

Das Foto unten sowie die Detailansicht im Eingangsbild zeigt den Murmeladdierer des HNF in voller Schönheit, den Kugelspender von Leibniz könnte man oben drauf setzen (Foto: Jan Braun, HNF). Im Prinzip stellt der Addierer aber schon einen Multiplizierer dar, denn Kugeln lassen sich auch von Hand einwerfen. Bei einer Rechnung wie 1011 x 11 bzw. 11 x 3 gibt man ins Gerät drei Kugeln bei 1, 2 und 8 ein und in der zweiten Runde bei 2, 4 und 16. Heraus kommt das Produkt 100001 in binärer oder 33 in dezimaler Schreibweise.

Zum Schluss möchten wir noch an einen modernen Dualrechnererfinder erinnern, Raymond Valtat. Er meldete 1931 ein französisches und 1932 ein deutsches Patent für einen binären Multiplizierer an. Die deutsche Patentschrift ist auf der Website des Patentamts einsehbar, wenn man „Rechenmaschine“ ins Titel- und „Valtat“ ins Namensfeld tippt. Leider unterschlug der Franzose manche Einzelheit der Erfindung, jeder Leser ist aber aufgefordert, sich an einer Realisierung zu versuchen.