Rechnen mit allen Tricks

Von heute bis zum Sonntag richtet das HNF die Weltmeisterschaft im Kopfrechnen aus. Es nehmen 43 Denker und Denkerinnen teil, darunter zehn aus Indien. Im Folgenden stellen wir Verfahren zum Rechnen im Kopf oder auf dem Papier vor, die nur selten in der Schule gelehrt werden: die Trachtenberg-Methode, die vedische Mathematik und die japanische Multiplikation.

Der erste Meister des Kopfrechnens war Jedediah Buxton. Er gewann keinen Preis, wurde jedoch 1754 von Wissenschaftlern der Royal Society in London getestet. Im April 2024 gab es eine Weltmeisterschaft in jener Disziplin, die gleichfalls in London stattfand, und heute startet im HNF der World Cup. Er endet am Sonntag; am Samstag kann man um 17 Uhr schon eine Rechen-Show besuchen.

Wie man sich denken kann, gehen die Teilnehmer solcher Wettbewerbe nicht so vor, wie wir es beim gewohnten schriftlichen Rechnen tun. Neben den Methoden, die wir in der Schule erlernten. führen noch ganz andere Wege zu einem mathematischen Resultat. Drei möchten wir näher untersuchen. Der erste stammt von einem Mann, der am 17. Juni 1888 im ukrainischen Odessa geboren wurde; damals gehörte die Stadt am Schwarzen Meer zum Zarenreich. Er hieß Jakow Trachtenberg.

Jakow Trachtenberg 1940 (Foto Wiener Stadt und Landesarchiv, Gestapo, K1 CC BY-SA 4.0 seitlich beschnitten)

Trachtenberg studierte in Sankt Petersburg die Ingenieurkunst; danach arbeitete er im Obuchow-Werk, einem großen Stahlbetrieb. 1919 emigrierte er wie viele seiner Landsleute nach Berlin. 1934 floh er vor den Nazis nach Österreich und später nach Jugoslawien. Den Zweiten Weltkrieg verbrachte er in deutschen Gefängnissen und Lagern; dort entwickelte er sein Rechensystem. Ab 1945 lebte er in der Schweiz, gab Sprach- und Mathematikkurse und schrieb ein „Lehrbuch des praktischen Schnellrechnens für jedermann“. Jakow Trachtenberg starb am 26. Oktober 1951 in Zürich.

Sein Lehrbuch war eine Sammlung vieler Rechentricks. Ein Beispiel ist die Multiplikation mit der Zahl 6, wobei alle Ziffern der Ausgangszahl gerade sind. Man geht von rechts nach links durch diese Zahl und erhöht jede Ziffer um die Hälfte der rechten Nachbarin, dazu kommen eventuelle Überträge. Eine zweite Regel betrifft Zahlen, die auch ungerade Ziffern enthalten. Dieses Video in deutscher Sprache stellt das Verfahren gut dar; das komplette Trachtenberg-System liefert die amerikanische Ausgabe seines Lehrbuchs von 1960. Sie steht ohne Anmeldung im Internet Archive zur Verfügung.

Kreuzmultiplikation 56 x 23 = 1.288 – die Linien zeigen jeweils die Zwischenprodukte an.

1965 erschien in der indischen Stadt Varanasi, ebenso als Benares bekannt, ein Buch mit dem Titel Vedic Mathematics. Sein Autor Bharati Krishna Tirtha wurde 1884 in Südindien geboren, von 1925 bis zu seinem Tod im Jahr 1960 lebte er in der Stadt Puri südwestlich von Kalkutta. Wir dürften ihn wohl als Guru bezeichnen. In seinem Buch berief er sich auf die Veden, religiöse Schriften des Hinduismus. Diese Herleitung wurde von anderen indischen Mathematikern kritisiert, doch mag es sein, dass Bharati Krishna Tirtha Kenntnisse von alter indischer Rechenkunst besaß.

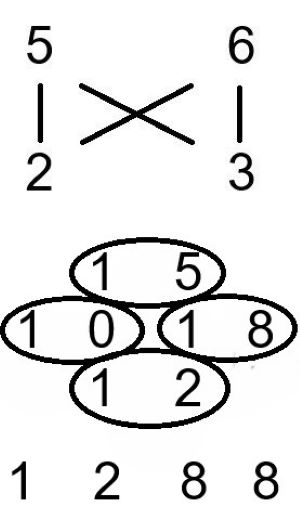
Seine Lehre umfasste auch die Multiplikation. Wir nehmen etwa die Aufgabe 56 x 23, die wir oben darstellen. Als Teilprodukte fallen dann 5 x 2, 5 x 3, 6 x 2 und 6 x 3 mit den Resultaten 10, 15, 12 und 18 an. Daraus ergeben sich mit den Zehnerpotenzen 1.000, 150, 120 und 18 und die Endsumme 1.288. Laut Wikipedia gilt die vedischen Regel „vertikal und kreuzweise“. Bei längeren Zahlen steigt die Zahl der Teilprodukte an, und in der grafischen Darstellung tauchen neben den Kreuzen noch Sterne auf.

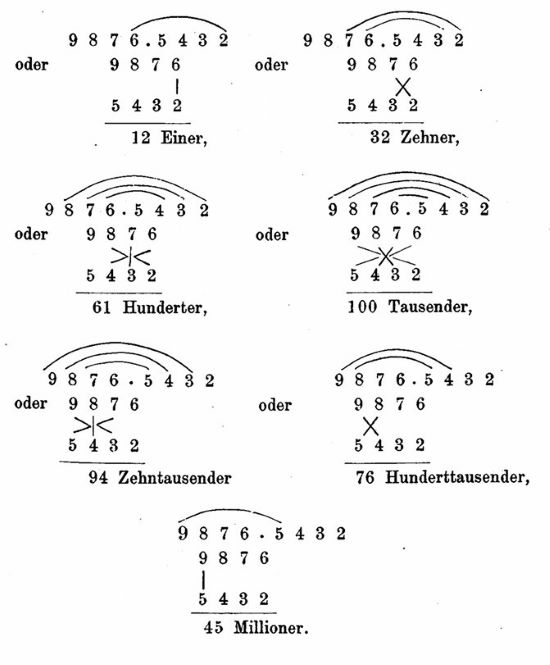
Indische Multiplikation in einem Schweizer Mathematikbuch von 1888 (C. E. Enholtz, „Lehrbuch der elementaren Mathematik zum Schul- und Selbstunterricht“)

Eine solche Rechentechnik war in Europa schon im 13. Jahrhundert bekannt; sie kam wohl über die arabischen Länder aus Indien. Die Kreuzmultiplikation – in der Fachliteratur heißt sie auch symmetrische Multiplikation – verbreitete sich während der Renaissance in Italien, sie verschwand aber nach einiger Zeit wieder. Zur Kaiserzeit versuchte der Berliner Fritz Ferrol, sie zu popularisieren, heute haben wir das Buch des verstorbenen Gurus. Bitte beachten: Neben der geschilderten Kreuzmultiplikation existiert noch ein Verfahren gleichen Namens zum Umformen von Brüchen.

Unser drittes Verfahren ist die japanische Multiplikation. Sie entstand vermutlich in den 2000er-Jahren, ihren Erfinder kennen wir nicht. Beim Rechnen drückt man die beiden Faktoren durch Gruppen von Linien aus, die sich gegenseitig schneiden. Die Anzahl der Linien einer Gruppe entspricht einer Dezimalziffer; das Endresultat folgt aus der Zahl der Schnittpunkte, wie es die Grafik unten zeigt. Man muss nun die einzelnen Punktmengen in Dezimalzahlen übertragen, spaltenweise summieren und unter genauer Beachtung der Stellenposition aufaddieren.

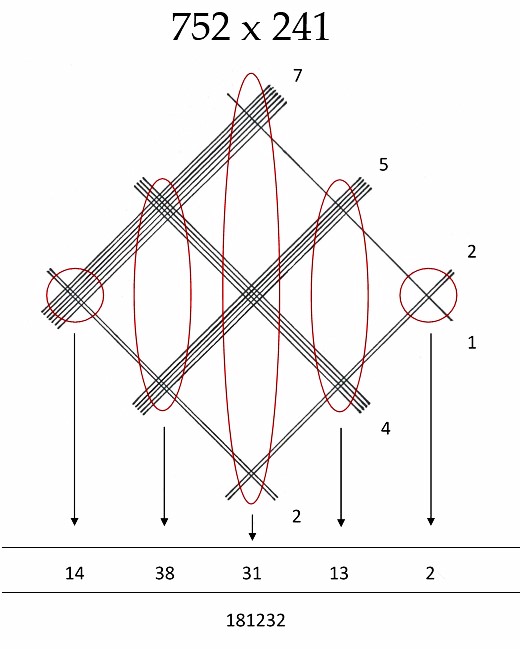
Angebliche japanische Multiplikation (Foto Andreas Egger CC BY-SA 4.0)

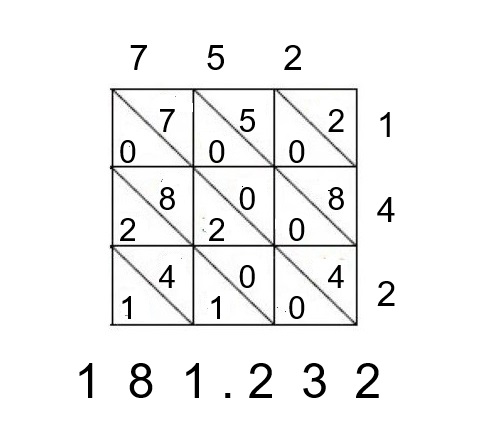
Eine informative Darstellung der Technik bringt eine Schülerarbeit aus dem Jahr 2019. Bei größeren Zahlen stößt sie aber schnell an ihre Grenzen. Sie ist eigentlich nur eine grafische und nicht sehr praktische Umsetzung der Gelosia- oder Gitter-Multiplikation. Diese hat ebenfalls arabisch-indische Wurzeln; hier geht zu einem Video dazu. Von den alternativen Rechenwegen gefällt uns die Gelosia-Methode immer noch am besten, selbst wenn sie sich nicht fürs Kopfrechnen eignet. Das Bild ganz unten zeigt in diesem Stil das obige Beispiel 752 x 241 = 181.232.

Wer das Kopfrechnen erlernen will, sollte den Wikipedia-Eintrag aufrufen, der auch Literatur nennt. 2013 erschienen die „Mathe-Tricks für alle Lebenslagen“ des SPIEGEL-Autors und Trachtenberg-Fans Holger Dambeck. Nach Anmeldung im Internet Archive kann man hier und hier „High-Speed Mathematics“ aus Amerika trainieren. Auf Englisch finden sich ebenso die „Rechenkniffe“, die der deutsche Mathematik-Erklärer Karl Menninger 1931 verfasste. Die Originalausgabe gibt es – zu teilweise gesalzenen Preisen – in Antiquariaten.

Gelosia-Multiplikation 752 x 241. Bitte beachten: in der klassischen Gitter-Multiplikation stehen die Einer unten, die Zehner darüber usw., und die Zwischenprodukte werden von rechts oben nach links unten aufsummiert.