Reise in die vierte Dimension

Der freie Raum besitzt drei Richtungen, die Länge, die Breite und die Höhe oder Tiefe. Eine vierte gibt es nicht. Oder vielleicht doch? Mathematiker und Physiker haben keinerlei Probleme mit der vierten Dimension, manchmal werden es auch mehr. Begleiten Sie uns also in die Welt, in der man für jeden Punkt mindestens vier Koordinaten braucht.

Friedrich Schiller drückte es am schönsten aus: „Dreifach ist des Raumes Maß. / Rastlos fort ohn‘ Unterlaß / Strebt die Länge fort in‘s Weite; / Endlos gießet sich die Breite; / Grundlos senkt die Tiefe sich.“ Das sagte er in den Sprüchen des Konfuzius. In der Wissenschaft heißt es etwas trockener: Der Raum besitzt drei Dimensionen, und jeder Punkt hat eine x-, eine y- und eine z-Koordinate. Wir sehen es im Alltag; seitdem es die Virtuelle Realität gibt, wird es auch im Computer programmiert.

Eine vierte Dimension können wir uns nicht vorstellen; lange Zeit war die Menschheit mit dreien zufrieden. Dann kam Gustav Theodor Fechner, Professor für Naturphilosophie und Anthropologie an der Universität Leipzig. Unter dem Pseudonym Dr. Mises brachte er 1846 ein Bändchen „Vier Paradoxa“ heraus. Das zweite Kapitel trug den Titel Der Raum hat vier Dimensionen; es suchte die oben erwähnte vierte. Fechner fand sie auch, aber nicht im geometrischen Raum. Die vierte Dimension war für ihn die Zeit.

Modell eines vierdimensionalen Tetraeders (5-Zell) nach Victor Schlegel. (Copyright 2019 Modellsammlung, Mathematisches Institut der Universität Göttingen)

Fechners Idee der kombinierten Raumzeit sprach Science-Fiction-Autoren an; so manche Zeitmaschine wurde darin auf den Weg gebracht. In Leipzig lehrte auch der Astronom Karl Friedrich Zöllner. Er deutete die vierte Dimension räumlich: er hielt sie für den Wohnsitz von Geistern. Mit Hilfe eines Spiritisten nahm er 1877 Kontakt zu ihnen auf. Sie entwirrten für ihn Knoten in einer Schnur; anschließend beschrieb Zöllner seine Experimente in einem dicken Buch, das einen Riesenskandal auslöste.

1880 begann die seriöse Erforschung der Raumdimension. Der amerikanische Mathematiker Irving Stringham fertigte, wiederum in Leipzig, die ersten Zeichnungen vierdimensionaler Objekte an. Im gleichen Jahr verfasste der englische Lehrer Charles Hinton eine allgemein verständliche Darstellung. 1884 baute sein deutscher Kollege Victor Schlegel die ersten Modelle – siehe oben. Er hatte keinen direkten Einblick in die höhere Dimensionen, sondern stellte sich die Projektionen geometrischer Körper in die vertrauten drei vor.

Modell eines Hyperwürfels vor der Überführung in die vierte Dimension. (Copyright 2019 Modellsammlung, Mathematisches Institut der Universität Göttingen)

Das populärste 4D-Objekt ist der Hyperwürfel oder Tesserakt. Er entsteht durch Verlängern eines 3D-Würfels in die vierte Dimension. Erkennbar ist ein Schattenbild der 32 Kanten. Eine andere Darstellung geht von einem Bausatz aus; er vermittelt zumindest einen Eindruck vom finalen Tesserakt. Zunächst werden im dreidimensionalen Raum acht Kuben verbunden. Danach klappt man sieben der acht in der vierten Dimension nach oben und schließt den Hyperwürfel. Salvador Dali hat ihn in einem berühmten Gemälde verewigt.

In der 4D-Welt gibt es auch runde Sachen. Die Hypersphäre vereint alle vierdimensionalen Punkte, die zu einem festen Punkt eine bestimmte konstante Entfernung besitzen. Ihre Oberfläche ist ein gekrümmter dreidimensionaler Raum. Das hört sich schlimmer an als es ist. In jenem Raum geht es so zu wie in unserer Alltagswelt; er ist nach allen Richtungen offen. Dabei ist er nicht unendlich, sondern wiederholt sich immer wieder. Das zeigt sehr schön ein Video. Mathematische Gesetze wie das Parallelenaxiom gelten aber nicht.

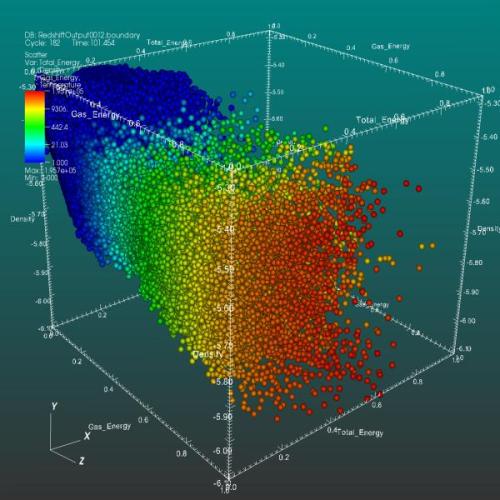
4D-Streudiagramm: drei Dimensionen werden für die Positionen der Datenpunkte benötigt, die vierte für einen weiteren Wert. Dieser wird über die Farbe codiert.

Auf diese Weise ahnen wir also, was an der Außenseite eines 4D-Körpers passiert. Zum Abschluss sei mitgeteilt, dass es Dimensionen nicht nur in der Geometrie, sondern ebenso im täglichen Leben gibt. Wenn wir mit vier Zahlenwerten hantieren, agieren wir in einem abstrakten Raum mit vier Dimensionen. Ein Beispiel ist der Farbraum im CMYK-Modell, der Palette der Druckfarben. Er basiert auf den Skalen für Cyan, Magenta und Gelb („Yellow“), dazu kommt eine vierte für den Schwarzanteil („Key“).

Ein anderer Fall: Orte in der Erdatmosphäre besitzen zwei Koordinaten und eine Höhe über dem Meeresspiegel. Jedem Ort können wir nun eine Temperatur zuweisen – damit haben wir wieder einen Raum mit vier Dimensionen. In der Meteorologie sind „4D Data“ das Normalste auf der Welt, für die es Software zum Visualisieren gibt. Wer aber mehr über die Schrecken der vierten Dimension erfahren will, dem empfehlen wir den Zaubergarten der Mathematik. Unser Thema steht im vorletzten Kapitel. Für die beiden Modell-Fotos bedanken wir uns bei Professor Laurent Bartholdi vom Mathematischen Institut der Universität Göttingen.