Herr Leibniz und sein Analogrechner

Gottfried Wilhelm Leibniz wird 2016 im ganzen Land gefeiert. Er erfand unter anderem die Differentialrechnung, das Dualsystem und die Rechenmaschine mit Staffelwalzen, aber auch ein Gerät zum Lösen algebraischer Gleichungen. Der Mathematiker Johann Andreas von Segner, der von Leibniz‘ Idee nichts wusste, erfand das Instrument ein zweites Mal; 1768 wurde es in England gebaut.

Seit dem 19. Januar 2016, dem Tag der Eröffnung in Schloss Herrenhausen zu Hannover, befinden wir uns im Leibniz-Jahr, das dem berühmten Gelehrten gewidmet ist und viele Veranstaltungen zu seinem Leben und Werk umfasst. Geboren wurde Gottfried Wilhelm Leibniz am 1. Juli 1646 in Leipzig. Sein Berufsleben verbrachte er zum größten Teil in Hannover, wo er am 14. November 1716 starb und 200.000 Blatt Papier hinterließ, darunter 15.000 Briefe von mehr als 1.000 Korrespondenten.

Wir verdanken Leibniz eine Fülle von Ideen zur Philosophie und zur Logik, doch sein wichtigstes Erbe ist die Differentialrechnung, die zur modernen Mathematik führte. Er beschrieb auch das Rechnen im Dualsystem und baute fürs Dezimalsystem eine Rechenmaschine mit Staffelwalzen, die zum ersten Mal die Multiplikation ausführte. Weniger bekannt ist sein mechanischer Analogrechner, den er im Dezember 1674 in zwei Manuskripten festhielt und später anderen Gelehrte in Briefen erläuterte. Publiziert oder gar realisiert hat er den Constructor – so nannte er seine Erfindung – aber nie.

Das Recheninstrument hat den Zweck, die Lösungen einer algebraischen Gleichung zu finden. Es soll also etwa das x aus ax + bx² + cx³ = d ermitteln. Wie geht das? Zuerst stellt man links am Constructor die Werte a, b und c ein und danach einen beliebigen Startwert für x. Diese Einstellungen verändern das Gestänge und bewirken, dass an der Seite eine Strecke der Länge ax + bx² + cx³ erscheint. Sie ist vermutlich noch nicht gleich d, durch Verschieben und Verdrehen von Stangen lässt sich x aber so verändern, dass ax + bx² + cx³ den Wert d annimmt. Und damit wäre unser Ziel erreicht.

Aufbau und Arbeitsweise des Constructors sind unten angedeutet. Die Grafiken stammen aus einem Artikel von Joseph Ehrenfried Hofmann „Über frühe mathematische Studien von G. W. Leibniz“, den die „Studia Leibnitiana“ in Heft 2/1970 brachten. Die Linien in den Bildern bezeichnen die Abstände der Elemente des Geräts, also der Schieber, Gelenke, Räder usw. Klar ist, dass man den Constructor vergrößern oder verkleinern kann, wobei die Mechanik sicherstellt, dass sich die Seitenverhältnisse der schraffierten Dreiecke nicht ändern.

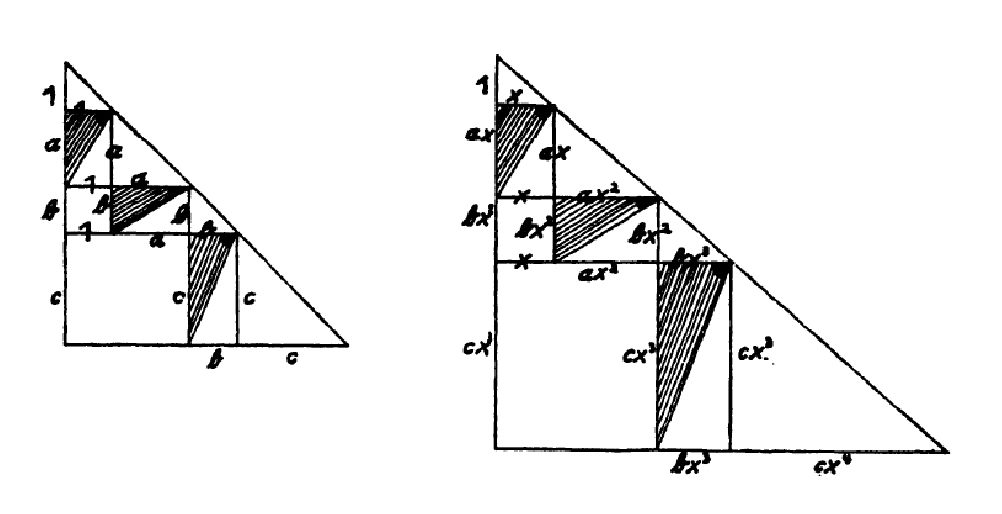
Das linke Bild zeigt den Constructor nach Einstellen von a, b und c; das kleine Dreieck ganz oben hat hier zwei Seiten der Länge 1. Das rechte Bild stellt den Zustand des Geräts nach Einstellen eines x-Wertes im Dreieck dar. Dieses x verändert das Gestänge, und die Seitenlängen der schraffierten Dreiecke werden mit x, x² und x³ multipliziert. Auf diese Weise erhalten wir an der linken Seite des großen Dreiecks eine Strecke der Länge 1 + ax + bx² + cx³, von der wir nun einfach die 1 abziehen.

Eines der Constructor-Manuskripte ist mittlerweile online. Auf den Seiten 28, 29 und 30 sehen wir Skizzen des Geräts von Leibniz selbst. Auch wer kein Latein versteht, merkt die Mühe, die er sich mit dem Instrument machte, und ahnt den Verdruss, mit dem er die Entwürfe in seiner Zettelwirtschaft ablegte. Doch wo ein Mathematiker aufgab, kommt ein anderer weiter und ein dritter zum Ziel; damit wären wir bei Johann Andreas von Segner aus Halle und John Rowning aus Anderby.

Segner wurde 1704 in Preßburg geboren, dem heutigen Bratislava, studierte in Jena und arbeitete als Arzt in seiner Heimatstadt. Ab 1732 lehrte er Mathematik in Jena, Göttingen und Halle, wo er 1777 starb. 1758 ersann er ein geometrisches Verfahren zum Lösen einer algebraischen Gleichung, das 1761 in Sankt Petersburg im Druck erschien. Dieses Verfahren stellt ein abstraktes Rechengerät dar, an dem man – um bei kubischen Gleichung zu bleiben – die Koeffizienten a₀, a₁, a₂ und a₃ und die Variable x eingibt und die Summe a₀ + a₁x + a₂x² + a₃x³ abliest.

Grafik: www.matheretter.de/geometrie/strahlensaetze

Segners Konzept erinnert so sehr an den Entwurf von Leibniz, dass wir von einer Neuerfindung des Constructors sprechen können. Ein Plagiat dürfen wir getrost ausschließen, da Leibniz‘ Papiere ihm nicht zugänglich waren. Im Detail war der neue Ansatz einfacher als der alte, weil der Preßburger Mathematiker auf geniale Weise den Strahlensatz anwandte. Der Satz ermöglicht eine geometrische Multiplikation wie oben gezeigt: Setzen wir a₂  gleich 1, dann folgt daraus b = a * b₂, und diese Rechnung finden wir mit anderen Buchstaben bei Segner wieder.

Die Analog-Experten Stefan Drechsler und Barbara Häberlin haben 2006 die Segnersche Methode in gut lesbarer Weise erläutert. Wir bitten unsere Leser, ihren Aufsatz zur Wurzelbehandlung zu studieren. Die beiden beschreiben, wie jene Methode 1768 in ein funktionsfähiges Modell umgesetzt wurde. Es stammte vom Engländer John Rowning, der nur wenig älter als Segner war und Mathematik und Philosophie in Cambridge studiert hatte. Im Hauptberuf wirkte er als Pfarrer im Städtchen Anderby an der englischen Ostküste.

Der Aufsatz von John Rowning ist ebenfalls online und enthält eine Zeichnung seines Instruments, von der wir unten einen Ausschnitt bringen. Heute existiert es nicht mehr, aber dafür entstanden 1992 zwei Neubauten. Verantwortlich waren die italienischen Forscher Franco Conti und Aldo Frediani, die Exponate für eine Mathematikausstellung suchten. Einige Jahre später erhielten sie ein Patent für eine „Macchina generatrice di polinomi“, die algebraische Gleichungen bis zur fünften Potenz von x darstellen kann.

Damit ist die jahrhundertelange Geschichte des Leibnizschen Analogrechners noch nicht vorbei, denn es fehlt der virtuelle Constructor in der Version von Segner. Dieser findet sich hier und liefert keine Zahlen, doch das Prinzip. Die Schieber ganz links haben die Abstände a₀, a_1, a₂ usw., und das unterste Gelenk auf der nach links und rechts versetzbaren x-Linie hat die Höhe a₀ + a₁x + a₂x² +…  über der Grundlinie. Mit dem Schalter „degree“ links oben lässt sich die höchste Potenz von x wählen.

Die schlechte Nachricht ist, dass wir nie ein x erhalten, das die Summe gleich 0 werden lässt, von komplexen Werten mit der gefürchteten Wurzel aus -1 ganz zu schweigen. Der Constructor bleibt eine mathematische Spielerei, die aber Spaß macht. Wer sich für weitere solcher Spielzeuge interessiert, findet im Netz noch zwei Übersichtsartikel in englischer Sprache aus den Jahren 1905 und 1945.