Der fleißige Biber der Informatik
Geschrieben am 08.07.2025 von HNF
Die Turing-Maschine zählt zu den Grundlagen der Informatik; sie ist das einfachste Modell einer Rechenanlage. 1962 entwarf der ungarisch-amerikanische Mathematiker Tibor Radó ein Programm für sie, das er „Fleißiger Biber“ nannte. Sie schreibt damit möglichst viel und hält an. 2024 wurde bewiesen, dass ein fleißiger Biber mit fünf Programmzeilen 4.098 Zeichen zu Papier bringen kann.
Die Turing-Maschine ist eine Idee des englischen Mathematikers Alan Turing, der sie 1936 in einem Beitrag für eine Fachzeitschrift definierte. Die Maschine setzt Zeichen auf ein Band oder löscht sie; dabei folgt sie einem Programm mit mehreren Befehlen. Alternativ kann man ihr Verhalten durch Zustände beschreiben, die sie annimmt. Im Computerzeitalter zog die Turing-Maschine auch in die theoretische Informatik ein.
1962 erschien in den USA ein Artikel zu solchen Maschinen, der den Titel trug „Über nicht-berechenbare Funktionen“. Sein Verfasser Tibor Radó wurde 1895 in Budapest geboren. Er kämpfte im Ersten Weltkrieg für Österreich-Ungarn, geriet in russische Gefangenschaft und floh 1920 aus einem Lager in Sibirien. In den 1920er-Jahren studierte er Mathematik in Ungarn, nach Forschungen in Deutschland ging er 1929 in die USA. Ab 1930 lehrte er an der Universität des Bundesstaats Ohio, dort entstand dieses Foto. Er starb 1965 kurz nach seiner Pensionierung.
Mathematikertreffen 1928 im ungarischen Szeged; Tibor Radó hockt links unten.
Im Artikel von 1962 führte Radó ein Spiel namens Busy Beaver ein; zu Deutsch „Fleißiger Biber“. Man musste dabei ein Programm für eine Turing-Maschine finden, die ein Band mit Nullen bearbeitete. Die Maschine schrieb in ein Feld eine 0 oder eine 1 und rückte danach ein Feld nach links oder rechts. Vorgegeben war die Zahl der Programmzeilen – Radó sprach von „Karten“. Sieger wurde die Befehlsliste, mit der die Turing-Maschine die größte Zahl von Einsen zu Papier brachte und danach stoppte. Da sie beim Ausführen des Programms auch Ziffern überschrieb, war die Zahl der vollzogenen Arbeitsschritte natürlich größer.
Die erste Biber-Konkurrenz startete Tibor Radó mit seinem Artikel. Ein von ihm zitiertes Programm umfasste drei Zeilen und schrieb sechs Einsen nacheinander. 1965 zeigten Rado und einer seiner Studenten, dass dies die längste Ziffernfolge ist, die eine Turing-Maschine mit drei Zuständen produziert. Unendliche Folgen – sie entstehen mit einer Schleife im Programm – schließen wir hier aus. 1966 erdachte der amerikanische Mathematiker Allen Brady einen fleißigen Biber, der mit vier Befehlszeilen dreizehn Einsen erzeugte. Später bewies er, dass kein besserer in dieser Klasse existiert.
Anfang 1983 fand in der Universität Dortmund – heute TU Dortmund – eine Tagung der Gesellschaft für Informatik statt. Sie widmete sich der theoretischen Informatik und lobte einen Wettbewerb für fleißige Biber mit fünf Zuständen aus. Es trafen 133 Programme ein, die ein Siemens-7.748-Computer überprüfte. Die siegreiche Befehlsliste schickte Uwe Schult aus Hamburg; sie zeichnete 501 Einsen auf das Turing-Band. Ende 1984 schuf George Uhing in New York aber ein Programm mit fünf Zeilen, das 1.915 Zeichen schaffte.
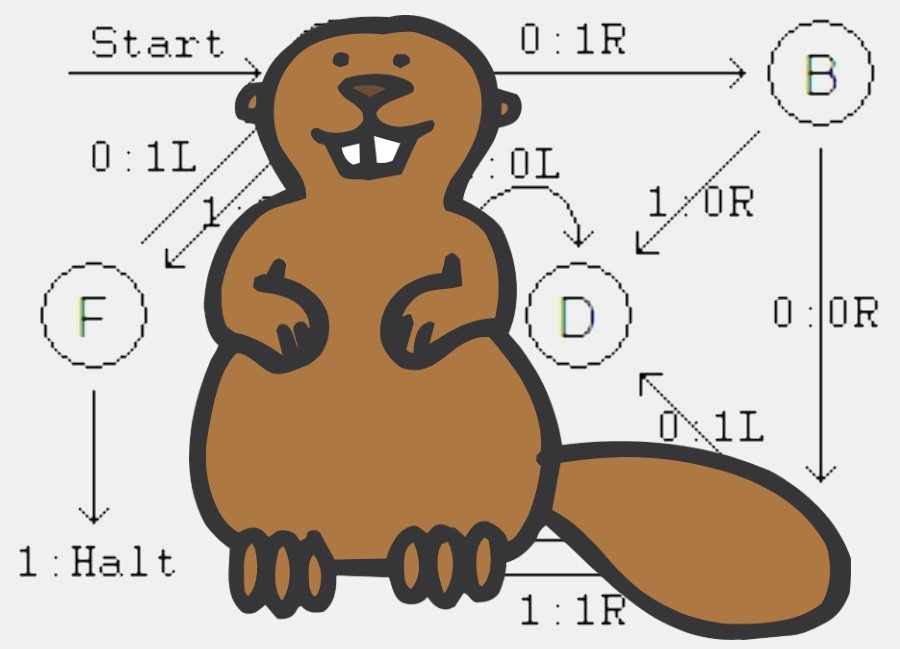
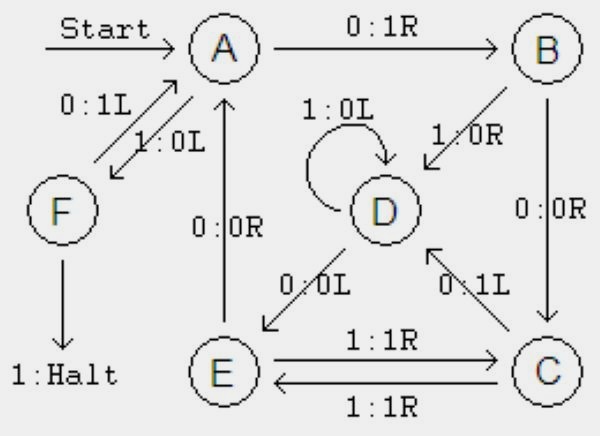
Der fleißige Biber von Heiner Marxen und Jürgen Buntrock, der 47.176.870 Schritte vollzog. Links stehen für jeden Zustand der Turing-Maschine die Befehle für eine 0 auf dem Feld, rechts die für eine 1. Genannt wird das neue Symbol, der nächste Schritt nach links oder rechts auf dem Band und der nächste Zustand. Der Stern ist das Stoppzeichen.
Eine neue Ära der Biber-Forschung brach 1990 an. Damals publizierten die in Berlin tätigen Informatiker Heiner Marxen und Jürgen Buntrock zwei Fünf-Zeilen-Programme, die 4.098 Einsen ausgaben. Das eine unternahm 11.798.826 Schritte, das andere stoppte nach 47.176.870 Aktionen. Jedoch wurde erst im Juli 2024 nachgewiesen, dass es wirklich das fleißigste Programm dieser Größe war. Dazu untersuchte die zwei Jahre zuvor gegründete Online-Gruppe The Busy Beaver Challenge 88.664.064 Turing-Maschinen.
Seit 2024 läuft die Jagd nach BB(6), wie fleißige Biber mit sechs Zeilen abgekürzt werden. Was treibt die Jäger außer sportlichem Ehrgeiz und akademischen Würden an? Ein Motiv mag sein, dass die Zahl der Biber-Einsen für n Programmzeilen ein schönes Beispiel einer nicht-berechenbaren Funktion f(n) darstellt; das gilt trotz der jüngsten Beweise für den Fünfer-Biber. Nicht-Berechenbarkeit meint in der Logik und der theoretischen Informatik das Fehlen eines allgemein verwendbaren Algorithmus.
Zweitens gibt es Verbindungen zwischen fleißigen Bibern und mathematischen Rätseln wie dem Collatz-Problem und der Goldbachschen Vermutung. Hier können wir Neugierige nur bitten, Experten zu fragen oder die Literatur zu konsultieren. Ein guter Einstieg wäre dieser Artikel – bitte die Links beachten. Die Busy-Beaver-Seite von Heiner Marxen ist inzwischen etwas angestaubt, hat aber auch viele Links. Waidmannsheil!
Grafische Darstellung eines fleißigen Bibers von Heiner Marxen und Jürgen Buntrock mit sechs Befehlszeilen oder Zuständen
Danke für den Beitrag zum Busy Beaver. An den GI Fachtagungen habe ich mehrfach teilgenommen und auch am Wettbewerb der GI. Mein „fleissiger Biber“ lief auf dem HP Tischrechner und terminierte nicht innerhalb von 8h. Deshalb wurde die TM von mir abgebrochen. Die TM war in BASIC geschrieben und es gab keine Analyse Werkzeuge auf dem HP Tischrechner. Dahre hatte ich nur die laufende Ausgabe der Programmschritte, die bei etwas 28.000 lag. Trotzdem habe ich das Programm für den Wettbewerb eingereicht. Von TMs hatte ich keine Ahnung, im Gegensatz zu den Preisträgern, die sich bereits Jahre mit dem Problem beschäftigt hatten, siehe auch der Bericht vom Wettbewerb von Ludewig, Schult und Wankmüller. PS Auf den Tagungen der GI traf man hin und wieder Konrad Zuse an, mit dem ich nach seinem Vortrag kurz sprechen konnte. Ein Highlight der frühen Anfänge meiner IT-Karriere.