Herr der unmöglichen Welten
Geschrieben am 28.11.2025 von HNF
Der Grafiker, Bildhauer und Hochschullehrer Oscar Reutersvärd erfand die unmöglichen Figuren. Er kam am 29. November 1915 in Stockholm zur Welt und starb am 2. Februar 2002. 1934 schuf er sein erstes Bild, das die Geometrie auf den Kopf stellte. Bekannter wurden aber ähnliche Werke des Künstlers M. C. Escher und des Mathematikers Roger Penrose.
Wie man weiß, wird der zu spät Kommende vom Leben bestraft. Manchmal trifft es auch den Frühstarter. Genau das passierte dem schwedischen Künstler Oscar Reutersvärd. Geboren am 29. November 1915 in Stockholm, entwarf er 1934 ein Gebilde, das die Gesetze der Geometrie verhöhnte. Die neun Würfel, aus denen es bestand, formten ein Dreieck im Raum, konnten aber niemals in der Realität existieren. Die Gruppe war eine unmögliche Figur.

Unmögliches Reutersvärd-Dreieck aus elf Würfeln (Foto Cmglee CC BY-SA 4.0 gekippt)
Vorläufer solcher Figuren tauchten in der Kunstgeschichte auf, so bei William Hogarth, bei Giovanni Battista Piranesi oder bei Marcel Duchamp. Reutersvärd war der Erste, der ihre Prinzipien erkannte und ihre Fülle erfasste. In seiner Karriere soll er mehr als 2.500 Stück gezeichnet haben. Er studierte unter anderem in Paris und arbeitete als Grafiker und Bildhauer. Ab 1953 lehrte er an der Universität Stockholm. 1964 erhielt er eine Professur für Kunstgeschichte im südschwedischen Lund. Dort starb er am 2. Februar 2002.
Oscar Reutersvärd war der Urheber der genannten Figuren, den Ruhm schöpften andere ab. An erster Stelle steht der niederländische Grafiker M. C. Escher. Ohne von Reutersvärd zu wissen, schuf er 1953 die Lithographie „Relativität“, man sieht sie hier oben in der Mitte. Der englische Forscher Roger Penrose fand sie in der Escher-Ausstellung, die 1954 beim großen Mathematiker-Kongress in Amsterdam stattfand. Zusammen mit seinem Vater entwickelte er daraus das Penrose-Dreieck und die Penrose-Treppe und veröffentlichte beide 1958.

Oscar Reutersvärd 1986 in Lund (Foto Michael Normann CC BY 4.0 seitlich beschnitten)
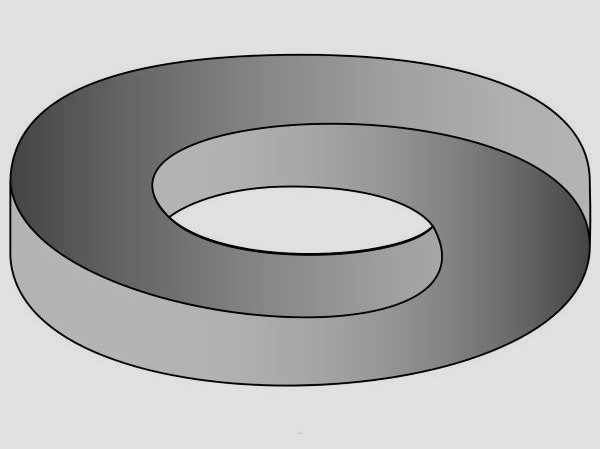
Was macht eine Figur unmöglich? In der Regel ist es eine falsche Verbindung. In unserem Eingangsbild – es folgt einem Reutersvärd-Entwurf – verläuft ein hochkant stehender Ring durch ein horizontales Brett. Die Schnittstellen passen nicht zur Orientierung, es dürfte nur eine Kreuzung geben. Der Zeichenstift erschafft zwei. Das Grundprinzip erklärt auch eine Animation. Bei den Reutersvärd-Würfeln weisen die Enden der Reihe, wenn man irgendwo einen Würfel wegnimmt, in verschiedene Richtungen. Der Künstler schließt sie kurz.
Ähnlich funktioniert die Wassermühle von M. C. Escher. Der SPIEGEL würdigte ihn 1972 in einem Artikel, für Reutersvärd war 1983 nur eine kurze Erwähnung drin, als drei seiner Figuren auf schwedischen Briefmarken landeten. 1984 erschien aber in einem bayerischen Verlag ein Sammelband mit Reutersvärd-Grafiken; er ist in Bibliotheken und Antiquariaten erhältlich. Eine persönliche Internet-Seite zum Künstler scheint es nicht zu geben, einen Einstieg in seine Werke liefert diese Website.
Sein Nachlass verteilt sich auf schwedische Archive. 350 Zeichnungen und einen dicken Briefwechsel besitzt die Lilly Library der Indiana University; Oscar Reutersvärd stand zu Lebzeiten in Kontakt mit dem niederländischen Wissenschaftler und Wissenschaftsautor Hans de Rijk, besser bekannt als Bruno Ernst. Er schrieb auch das Buch „Abenteuer mit unmöglichen Figuren“; man kann es nach Anmeldung im Internet Archive lesen. Das beste neuere Werk über Reutersvärd dürfte das von Chris Mortensen aus dem Jahr 2022 sein.
Die Literatur zu den unmöglichen Figuren ist inzwischen unübersehbar. Hier gibt es eine Einführung in deutscher Sprache. Das Illusoria-Land öffnet an jedem Sonntag nordöstlich von Bern; gegründet hat es der Schweizer Maler Sandro Del-Prete. Sein Buch lässt sich ebenfalls im Internet Archive studieren. In Berlin kann man das Illuseum und das DejaVu Museum besuchen, ein Museum der Illusionen und ein Paradox Museum stehen in Hamburg, weitere Illusionsmuseen bieten Stuttgart und Ückeritz auf Usedom an.