Multiplizieren einmal anders

In dieser Woche ist Paderborn Hauptstadt der deutschen Mathematik. Vom 5. bis 9. März halten die Deutschen Mathematiker-Vereinigung und die Gesellschaft für Didaktik der Mathematik in der Universität ihre gemeinsame Jahrestagung ab. Deshalb behandeln wir ein Thema aus der Rechenkunst, die neuartige Multiplikationstechnik des russischen Mathematikers Anatoli Karazuba. Sie ist schneller als die altbekannten Verfahren.

Wer kennt sie nicht, die vier Grundrechenarten, auch vier Spezies genannt. Addition, Subtraktion, Multiplikation und Division begleiten uns seit den ersten Schuljahren, und wohl jeder beherrscht die Techniken, um aus zwei Inputs einen Output zu gewinnen. Man fasst sie gewöhnlich unter der Bezeichnung „Schriftliches Rechnen“ zusammen.

Die lange Geschichte der Mathematik zeigt uns, dass es für das Malnehmen mehr als ein Verfahren gibt. Neben der Standardmethode existiert die Gelosia-Multiplikation: Hierbei werden alle Zwischenprodukte in einem Gitter notiert und ihre Ziffern in schrägen Reihen zusammengezählt. Der dritte Weg ist die russische Bauernmultiplikation; sie wird ebenso den Ägyptern und Abessiniern zugeschrieben. Sie läuft auf die Umwandlung eines Faktors in die entsprechende Dualzahl und sukzessives Verdoppeln des anderen Faktors hinaus.

1960 erfand ein russischer Student ein neues Verfahren. Der 23-jährige Anatoli Karazuba nahm in Moskau an einem Seminar des berühmten Mathematikers Andrei Kolmogorow teil. Es ging um die minimale Zahl von Rechenschritten, die bei einer Multiplikation anfallen. Karazuba entdeckte dabei einen lange übersehenen Trick, der eine entscheidende Reduktion ermöglichte. Kolmogorow veröffentlichte das Verfahren im Jahr 1962, ohne Karazuba zu fragen. Es ist inzwischen als Karazuba-Algorithmus bekannt.

Gelosia-Multiplikation  345 x 437 (senkrecht)

Ein einfaches Beispiel: Was ist 67 x 89 ? Die Zahl der Rechenoperationen lässt sich ablesen, wenn wir die Aufgabe etwas umwandeln:  (6 x 10 + 7) x (8 x 10 + 9)   Ausgeschrieben ergibt sich   6 x 8 x 100 + 6 x 9 x 10 + 7 x 8 x 10 + 7 x 9.  Das macht   4.800 + 540 + 560 + 63   und zusammen 5.963. Wir brauchen also vier Multiplikationen und drei Additionen. (Malnehmen mit 10 und 100 zählen wir nicht als eigene Operation.) Es erscheint müßig, bei der Rechnung irgendeinen Schritt einsparen zu wollen.

Anatoli Karazuba gelang es. Er betrachtete den Mittelteil der Summe,  6 x 9 x 10 + 7 x 8 x 10 oder kürzer  (6 x 9 + 7 x 8) x 10. In der Klammer setzte er zwei Terme hinzu, die er woanders abzog: (6 x 8 + 6 x 9 + 7 x 8 + 7 x 9) x 10 – 6 x 8 x 10 – 7 x 9 x 10. Der Klammerinhalt lässt sich nun – das war der Geniestreich – in ein Produkt umwandeln:  (6 + 7) x (8 + 9) x 10.  Am Ende erhalten wir   6 x 8 x 100 + (6 + 7) x (8 + 9) x 10 + 7 x 9 – 6 x 8 x 10 – 7 x 9 x 10  oder mit Zwischenprodukten   4.800 + 2.210 + 63 – 480 – 630.  Was ebenfalls gleich 5.963 ist.

Die Rechnung umfasst fünf Multiplikationen, zwei Additionen und zwei Subtraktionen. Die Terme hinter den Minuszeichen, 6 x 8 und 7 x 9, hatten wir zuvor aber schon ausgerechnet, sodass unterm Strich nur drei Multiplikationen stattfinden. Additionen und Subtraktionen sind vom Rechenaufwand vergleichbar und nicht so aufwändig wie Multiplikationen. Der Karazuba-Algorithmus ist deshalb schneller zu bewerkstelligen als die traditionelle Methode, um das Produkt zweier Zahlen zu ermitteln.

Anatoli Karazuba in jungen Jahren       (Foto Riemann, CC BY-SA 1.0)

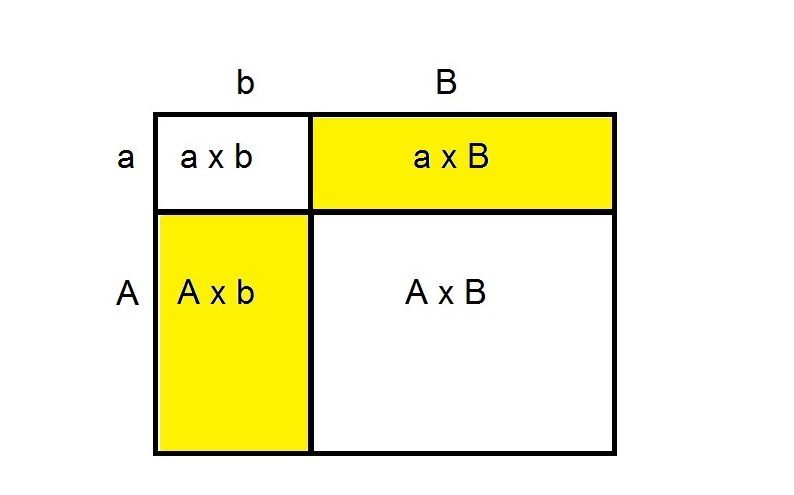
Generell werden zwei zweistellige Zahlen aA und bB mit den Ziffern a, A, b und B wie folgt multipliziert: a x b x 100 + (a + A) x (b + B) x 10 + A x B – a x b x 10 – A x B x 10. In unserem Eingangsbild ist die entscheidende Berechnung dargestellt. Anatoli Karazubas Verfahren eignet sich aber nicht zur schnellen schriftlichen Multiplikation. Die Ziffernsummen a + A und b + B können größer als 10 werden, und das erschwert das Kopfrechnen. Seine Vorzüge spielt es primär bei der Multiplikation von langen Zahlen in einem Computer aus.

Nunmehr deuten wir a, A, b und B nicht als Ziffern, sondern als Ziffernfolgen. Nehmen wir 234.567 x 456.789. Das wird zunächst in die Form (234 x 1.000 + 567) x (456 x 1.000 + 789) gebracht. Die weiteren Operationen verlaufen analog zum oben erklärten Fall mit 67 x 89. Die Mathematiker bezeichnen solche Aufspaltungen mit dem Ausdruck Teile und herrsche; sie lassen sich endlos erweitern. Bei längeren Zahlen wird der Karazuba-Algorithmus iterativ auf die einzelnen Teilaufgaben angesetzt.

Mittlerweile gibt es den Algorithmus natürlich im Internet, und wer einmal zwei richtig lange Zahlen multiplizieren möchte, kann es hier tun. Die anfangs genannte Tagung findet unter Ausschluss der Öffentlichkeit statt – Mathematik ist eben doch eine Geheimwissenschaft. Nur am Donnerstag, den 8. März, gibt es eine Veranstaltung über Mathematik in Industrie und Gesellschaft. Dort darf laut Pressemitteilung auch interessiertes Publikum hinein.