Vier Farben reichen

Computer haben sich öfter verrechnete, wegen Fehlern in der Software oder weil ein falsch programmierter Algorithmus im Prozessor Unsinn erzeugte. Dürfen wir also einem Computer trauen, der ein mathematisches Rätsel löste? Die Frage quält Informatiker und Mathematiker seit 1978, als ein Rechner des Typs IBM 370 das berühmte Vierfarbenproblem knackte, was zuvor keinem Menschen gelang.

Zu den schönsten Rätseln der Mathematik zählt das Vierfarbenproblem, das der Engländer Francis Guthrie, der später Professor in Südafrika wurde, 1852 als Student in London entdeckte. Man stelle sich eine echte oder fiktive Landkarte mit beliebig vielen Ländern vor, die alle möglichen Formen haben dürfen. Kann man mit höchstens vier Farben diese Länder so ausmalen, dass benachbarte Gebiete stets unterschiedlich getönt sind, oder braucht man mehr?

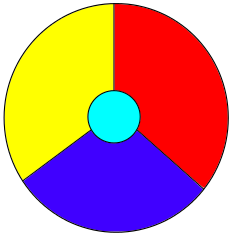
Fourcolorsmap.png, CC BY-SA 3.0

Das Bild oben zeigt, dass drei Farben zum Kartenfärben nicht reichen, die Frage ist also, ob fünf Farben zu viel sind. Dabei dürfen Länder, die nicht aneinander grenzen, durchaus gleiche Farben erhalten. Länder mit voneinander getrennten Territorien – wie die USA mit Alaska – und solche auf einer Kugel oder einem Torus seien ausgeschlossen.

Der Kieler Mathematiker Heinrich Heesch, der von 1955 bis 1975 in Hannover lehrte, gab als Erster einen Weg an, um die Frage zu klären. Allerdings hätte er, um seinen Lösungsweg bis zum Ende zu gehen, einen sündhaft teuren Computer benötigt. Von 1967 bis 1971 war er mehrmals in den USA, wo solche Rechner standen, doch die Deutsche Forschungsgemeinschaft strich das Geld, das er zum Abschluss seines Projekts gebraucht hätte.

Die gute Nachricht ist, dass der in Berlin geborene Mathematiker Wolfgang Haken, der 1953 in Kiel promovierte und Heesch kannte, seit 1965 an der University of Illinois tätig war. Er und sein Kollegen Kenneth Appel entwickelten Heeschs Ideen weiter und ließen 1976 einen IBM-Computer des Systems /370 (Modell 168) 1.200 Stunden sein Beweisverfahren durchrechnen. Wichtigster Teil war die Prüfung von knapp 2.000 hypothetischen Landkarten.

Am Ende zeigte sich: Jede denkbare Karte lässt sich mit nur vier Farben färben. Zur Feier des Tages gab die amerikanische Post einen Sonderstempel Four colors suffice heraus – vier Farben reichen.

TeesJ, CC BY-SA 4.0

Doch könnte sich die IBM nicht verrechnet haben? Darf man einem Beweis trauen, den ein Mensch nicht am Schreibtisch nachvollziehen kann? In den frühen 1980er Jahren kamen Zweifel an der Korrektheit auf, und Haken und Appel mussten sich erneut an die Arbeit machen. Ihr Buch „Every Planar Map is Four-Colorable“ von 1989 besänftigte die Kritiker, und Kollegen verbesserten den Beweis, doch waren auch sie auf Computerhilfe angewiesen. Die Forschergemeinde hat heute die Lösung des Vierfarbenproblems akzeptiert, ein Rest von Unzufriedenheit wird aber stets bleiben.

Weniger bekannt als das Vierfarbenproblem ist die Robbins-Vermutung, die – was nicht verwundert – nach dem amerikanischen Mathematiker Herbert Robbins benannt ist, der sie formulierte. Es handelt sich um eine Behauptung aus der Booleschen Algebra, die nur Experten interessiert, die aber 1996 als erster mathematischer Satz von einem Beweisprogramm bewiesen wurde. Ein solches Programm kommt völlig ohne menschliche Hilfe aus, es benötigt nur den Satz, den es beweisen soll, und das zugrundeliegende Axiomensystem.

Die Software, die die Robbins-Vermutung bestätigte, trägt den Namen Equational Prover oder EQP und eignet sich für Sätze der Prädikatenlogik, die mit den Axiomen für die Gleichheitsrelation erweitert wurde. Der Beweis von 1996 steht natürlich im Internet, aber wer ihm nicht traut, der kann seit 2014 Zuflucht zu einer menschgemachten und menschenfreundlichen („human-friendly“) Schlusskette nehmen, die auch zum Ziel führt.

Beitragsbild: Fibonacci, CC BY-SA 3.0