Jacob Leupold und die Rechentechnik

Vor 350 Jahren, am 22. Juli 1674, wurde in Planitz bei Zwickau Jacob Leupold geboren. Er arbeitete zuerst als Instrumentenbauer, in den 1720er-Jahren begann er eine umfassende Darstellung der Technik. Bis zu seinem Tod am 12. Januar 1727 legte er sechs Bände vor. Drei weitere erschienen posthum, darunter das „Theatrum Arithmetico-Geometricum“ über Rechengeräte und Messinstrumente. 

Das einzige Bild, das wir von ihm besitzen, zeigt ihn als Gelehrten mit einer riesigen Barock-Perücke. Geboren wurde Jacob Leupold am 22. Juli 1674 im sächsischen Planitz; der Ort gehört heute zu Zwickau. Jacob lernte von seinem Vater diverse Handwerke und besuchte die Lateinschule. Er studierte Mathematik, Philosophie und Theologie; das nötige Geld verdiente er durch Nachhilfekurse. Für Mathematik- und Mechanikstunden fertigte er seine ersten Instrumente an.

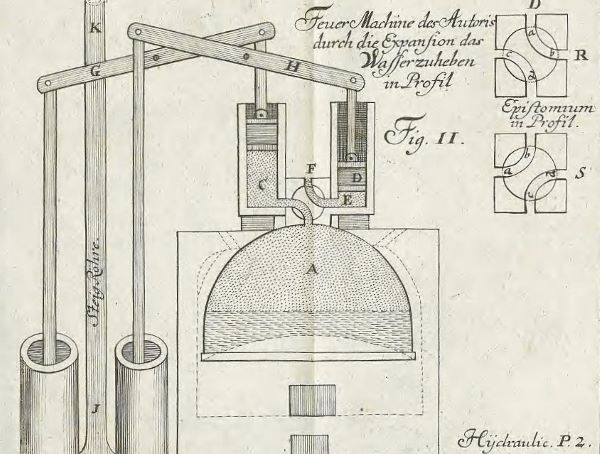
1702 brach Leupold das Studium ab und übernahm die Betriebsleitung eines Leipziger Krankenhauses. Die Arbeit ließ ihm genug Zeit für eine Werkstatt. Hier konstruierte er unter anderem Luftpumpen, die ein Vakuum erzeugten, und veröffentlichte Druckschriften. 1715 verließ er das Haus und gründete in der Stadt eine, wie er sie nannte, mechanische Fabrik. Sie führte Aufträge nach Kundenwünschen aus und lieferte etwa Feuerspritzen. Leupold erfand auch eine Dampfmaschine, die Wasser heben sollte.

Jacob Leupold

Ab 1720 widmete sich Jacob Leupold seinem Hauptwerk, dem „Theatrum machinarum“. Das Theater oder besser der Schauplatz war eine Serie großformatiger Bücher, die auf Deutsch und mit vielen Kupferstichen Zweige der Technik aufbereiteten. Die Idee war nicht ganz neu, bebilderte Darstellungen von zeitgenössischen Maschinen gab es schon im 16. Jahrhundert in Frankreich. 1712 hatte Leupold das Projekt im Entwurff Seiner Mechanischen Schrifften angekündigt; damals träumte er von insgesamt siebzehn Bänden.

Der erste erschien 1724 unter dem Titel „Theatrum machinarum generale“. Er behandelte die Grundlagen der Mechanik sowie Windmühlen, Wasserräder und Feuermaschinen. Leupold beschrieb ebenso die nötigen Rechenmethoden. Im selben Jahr folgten die Bände zum Wasserbau und der erste Teil der Hydraulik; Teil II lag 1725 vor. Danach kam der Schauplatz der Hebzeuge. Das Jahr 1726 sah die vier Teilbände des „Theatrum Staticum“ über Gewichts- und Wasserwaagen und zum Messen von Luft und Wind, außerdem brachte Leupold eine Einführung in den Brückenbau heraus.

Jacob Leupolds „Feuer-Maschine“, eine Dampfmaschine mit zwei Zylindern

Eine Liste der genauen Titel findet sich hier; die Bücher lassen sich leicht über Google Books oder im Internet Archive auffinden. 1726 vollendete Leupold wohl auch den siebten Band seiner Reihe, das Theatrum arithmetico-geometricum. Die Auslieferung ein Jahr später hat er nicht mehr erlebt, denn er starb am 12. Januar 1727 in Leipzig. Im Jahr 1739 erstellte der Grafiker Joachim Ernst Schäffler eine Edition seiner nachgelassenen Texte; 1767 endete das „Theatrum machinarium“ mit einem neu verfassten dreiteiligen Band zum Mühlenbau.

Uns interessiert natürlich der „Schau-Platz der Rechen- und Meß-Kunst“ von 1726/27. Das 26 Kapitel, 450 Paragraphen und 43 Kupfertafeln umfassende Werk enthielt die wahrscheinlich erste Übersicht über mathematische Geräte und Instrumente. Jacob Leupold begann mit dem Fingerrechnen und dem Abakus. Dort unterschied er die römische und die chinesische Form, der er neun Kügelchen pro Draht zuwies. Nach dem Rechentisch und der Rechentafel erläuterte er die Neperschen Stäbchen und darauf basierende Rechenvorrichtungen.

Leupolds Rechengerät nach dem Prinzip der Neperschen Stäbchen

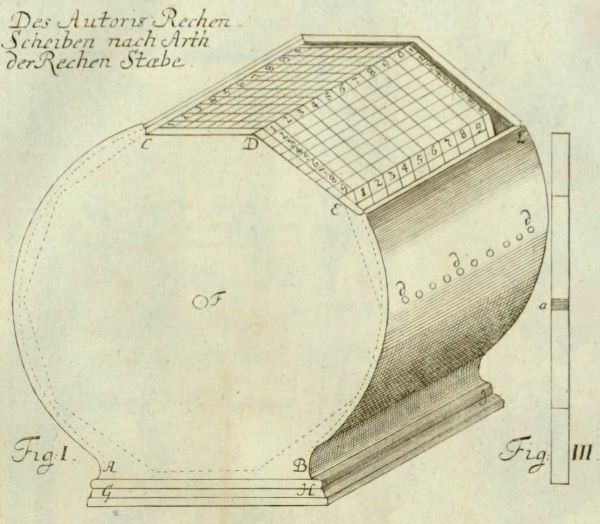
Hier entdecken wir Leupolds erste Maschine. Sie besteht, siehe Bild oben, aus zehn oder mehr Scheiben, die auf derselben Achse sitzen und separat gedreht werden können. Der schmale Rand jeder Scheibe ist in zehn Abschnitte unterteilt; jeder trägt die Ziffernpaare eines Neperschen Stäbchens. Wer zum Beispiel 357.916 mit der Zahl 4 multiplizieren will, muss sechs benachbarte Scheiben an die Positionen 3, 5, 7, 9, 1 und 6 bringen und aus den Paaren in der vierten Reihe das Ergebnis bilden.

Danach ging Leupold auf die Rechenmaschinen von Giovanni Poleni und Gottfried Wilhelm Leibniz ein. Hierbei stützte er sich auf einen Aufsatz von Poleni aus dem Jahr 1709 und einen Artikel von Leibniz von 1710. Poleni baute ein Multipliziergerät mit Sprossenrädern, das er dann wieder zerstörte; Leibniz beschrieb seine später verschollene „ältere Maschine“. Leupold erwähnte darüber hinaus sein Konzept für einen Rechenschieber. Er wusste auch von der Addiermaschine von Blaise Pascal, doch gelang es ihm nicht, nähere Informationen über sie zu erhalten.

Seine Rechenmaschine mit sechs Eingabe- und neun Resultatstellen

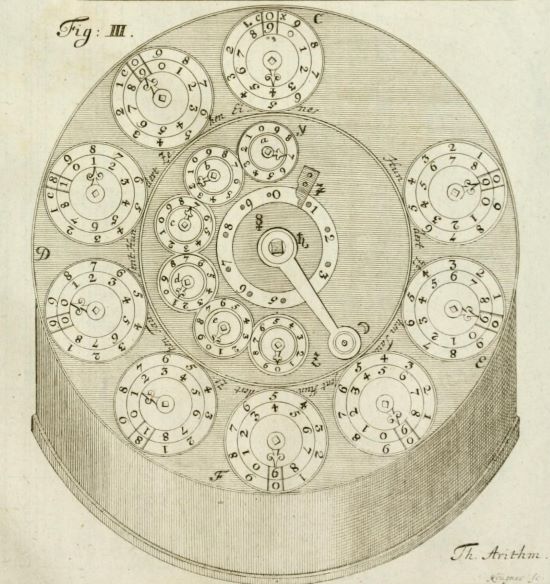
Dafür konnte er detailliert seine eigene zweite Rechenmaschine schildern; anscheinend stellte Leupold ein funktionsfähiges Modell her. Unser Eingangsbild zeigt die Realisierung des HNF des kompletten Geräts und von Teilen des Getriebes; es widmete dem Meister eine Vitrine im ersten Obergeschoss. Die Feinmechaniker Anton Braun und Philippe Vayringe setzten um 1730 den Entwurf in eine weitere Maschine um, die im Depot des Deutschen Museums liegt. Einen Nachbau besitzt das Bonner Arithmeum. Das Innenleben wird hier aufgeschlüsselt; bitte das Bild rechts unten auf der Seite anklicken.

Die digitalen Methoden und Maschinen füllen aber nur ein Fünftel des Buches. Der Rest betrifft analoge Verfahren im weitesten Sinne. Leupold führte eine Vielfalt von Linien und Skalen auf, die mit einem Zirkel abgegriffen werden, und den logarithmischen Rechenstab. Zwei Kapitel widmen sich dem Proportionalzirkel und eines dem Proportionallineal. Die Kapitel 19 bis 26 beschäftigen sich mit Reißzeugen und geometrischen Instrumenten aller Art, darunter einer Entwicklung von Jacob Leupold selbst.

Jacob Leupolds Vakuumpumpe aus dem Jahr 1709 steht heute im Mathematisch-Physikalischen Salom des Dresdner Zwingers. (Foto Derbrauni CC BY-SA 3.0)

An seinem 350. Geburtstag dürfen wir sagen, dass er zu den Pionieren der Technikpublizistik und der Informatik-Literatur zählt. Wir schließen mit seinem Lob der Rechenmaschine, das ebenso für Computer gilt: „Und obwohlen bey der Arithmetic vielen die Rechen-Machinen vor etwas überflüßiges und nicht allzunützliches scheinen dürfften […], so mögen selbige dargegen wohl erwegen, daß solche Machinen bey der Operation in Berechnung des Exempels niemahlen fehlen, und folglich man wegen der gesuchten Zahl gewiß seyn kan.“