Rechnen mit Seilen

Großrechner gab es schon vor 150 Jahren. Den ersten baute 1873 der Physiker Sir William Thomson, besser bekannt als Lord Kelvin; er ermittelte die Höhen der Gezeiten. Einen technischen Abkömmling konstruierte 1936 der amerikanische Ingenieur John Wilbur. Seine Maschine wog eine Tonne und löste lineare Gleichungssysteme. Eine handliche Ausgabe schuf der Bochumer Mathematiker Thomas Püttmann.

Bei Großrechnern denken wir meist an die Elektronengehirne der 1950er-Jahre oder an die Mainframes der Sechziger und Siebziger. Umfangreiche Rechengeräte sind aber älter. Im Blog schilderten wir die Anlage im Schifffahrtsmuseum Bremerhaven, die ab 1915 Ebbe und Flut voraussagte. Ihre Mechanik enthält vertikal verschiebbare Räder, über die ein langes Band läuft. Es summiert das Auf und Ab der Räder; die Bewegung des Bandendes liefert die Kurve der Gezeitenhöhen für einen Hafen.

Ein solches Gerät erfand um 1872 der britische Physiker Sir William Thomson, der 1892 zu Lord Kelvin wurde. 1873 stellte er den ersten Gezeitenrechner vor. Fünf Jahre danach sah er, dass man mit einer ähnlichen Technik ein mathematisches Problem angehen kann: die Lösung von linearen Gleichungen. Sie haben zum Beispiel die Form a * x + b * y + c * z = d . Wenn drei Gleichungen dieser Art zusammenkommen, dann lassen sich die Unbekannten x, y und z mit bestimmten Methoden ermitteln, etwa dem Gaußschen Algorithmus.

Der Nachbau von John Wilburs Gleichungslöser im Wissenschaftsmuseum von Tokio

Die Verfahren sind aber mühselig und langwierig. So entstand der Wunsch nach einer mechanischen oder elektrischen Prozedur. Gesucht wurde also ein Analogrechner, der nach Eingabe der Koeffizienten die Unbekannten ausgab. Wir überspringen das frühe Konzept von Sir William Thomson und gehen direkt in die 1930er-Jahre und ins Massachusetts Institute of Technology nahe Boston. Dort entwickelte der Assistenzprofessor John Wilbur Thomsons Ideen weiter. Er baute 1934 ein Modell für zwei Gleichungen mit zwei Unbekannten und 1936 einen Großrechner für maximal neun Gleichungen.

Wilbur wurde 1904 im Städtchen Oakland im US-Bundesstaat Maine geboren; 1933 machte er den Doktor am MIT. Auf die Tätigkeit als Assistenzprofessor folgte eine richtige Professur; von 1944 bis 1960 leitete Wilbur die MIT-Abteilung fürs Bauingenieurwesen. Er starb 1996. Sein Großrechner wog eine Tonne und war mehr als zwei Meter lang. In ihm saßen zehn Stahlplatten, die um die horizontale Achse gekippt werden konnten. Auf den Ober- und Unterseiten stellte man an verschiebbaren Rollen die Koeffizienten der Gleichungen ein.

Das Bild zeigt das Prinzip der Maschine für zwei Unbekannte. Auf jeder Platte lassen sich zwei Rollen verschieben, über die Seile laufen. Links oben werden die Seile herausgezogen – diese Technik erfand Thomas Püttmann in den 2010er-Jahren.  (Grafik Thomas Püttmann)

Über jene Rollen und über weitere ober- und unterhalb der Platten liefen Stahlbänder, die insgesamt 165 Meter lang waren. Sie wirkten auf die Anzeigen der Resultate. John Wilbur beschrieb seinen Simultaneous Calculator 1936 in einer Fachzeitschrift, ein schönes Foto brachte 1997 das Magazin Kultur & Technik. Es befindet sich auf PDF-Seite 27 – Achtung, dicke Datei! Für eine Rechnung mit neun Unbekannten und mit einer Genauigkeit von drei Dezimalstellen benötigte die Maschine bis zu drei Stunden.

Ein prominenter User war der Ökonom und spätere Nobelpreisträger Wassily Leontief. Er analysierte mit Wilburs Rechner Daten der amerikanische Wirtschaft und legte dazu 1941 ein Buch vor. Leider ging der Gleichungslöser nach dem Zweiten Welkrieg verloren. Der letzte Rest war eine der Stahlplatten für die verschiebbaren Rollen. John Wilbur lieh sie 1971 an die Ausstellung A Computer Perspective aus, sie ist im Begleitbuch abgebildet. Schon 1944 entstand aber ein Nachbau in Japan. Er lief in einem Luftfahrtforschungsinstitut; inzwischen kann man ihn im Wissenschaftsmuseum von Tokio besichtigen.

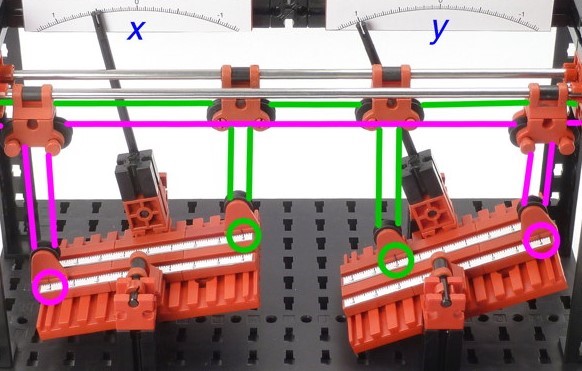
Die verschiebbaren Rollen entsprechen den Koeffizienten von x und y. Links erkennt man -4 und 4, rechts 4 und -2. Die Zeiger weisen auf die Lösungen hin.  (Foto Thomas Püttmann)

In den 2010er-Jahren schuf der Bochumer Mathematikprofessor Thomas Püttmann eine kleine Version der Wilbur-Maschine. Der Seilcomputer Kelvin bewältigte Systeme mit zwei Unbekannten, im Video findet er x und y für  4 * x – 2 * y = 0  und  -4 * x + 4 * y = 2 . Die Koeffizienten von x und y werden an den kippbaren Platten eingestellt, die Zahlen rechts vom Gleichheitszeichen mit den Kurbeln. Die Platten messen sechs mal neun Zentimeter. Die Werte für die Unbekannten x und y erscheinen auf den beiden Skalen.

2022 brachte Püttmann sein neues Buch Mathematik verstehen mit fischertechnik heraus; es beschreibt 28 Mathe-Modelle, darunter die letzte Version des Seilcomputers. Das Buch erklärt auch die geometrischen Grundlagen, die nicht über den Strahlensatz hinausgehen. Thomas Püttmanns Gerät ist oben in unserem Eingangsbild zu sehen, und wir bedanken uns bei ihm für die Fotos und die Grafik. Schon jetzt sei mitgeteilt, dass wir uns am Monatsende noch einmal mit Analogrechnern beschäftigen werden.

Die erste Version des Seilcomputers verwendete noch Zwirnsfäden. (Foto Thomas Püttmann)