
350 Jahre Dualsystem
Geschrieben am 26.05.2020 von HNF
Im Jahre 1670 – der Monat ist unbekannt – erschien im italienischen Campagna ein Buch mit dem Titel „Mathesis biceps, vetus et nova“, zu deutsch „Zweiköpfige Mathematik, alt und neu“. Autor war der Kirchenmann Juan Caramuel. Der gebürtige Spanier befasste sich auch mit der Wissenschaft; sein Werk enthält die erste gedruckte Darstellung des binären Zahlensystems.
Das Rechnen im Dualsystem, also nur mit den Ziffern 0 und 1, ist alt und ehrwürdig. Die Ägypter verwendeten vor 3.000 Jahren Kehrwerte von Zweierpotenzen. Sie kannten auch eine Rechenmethode, die implizit Dualzahlen benutzte. Bei uns nannte man sie die russische Bauernmultiplikation. Die alten Chinesen versteckten die Dualzahlen in dem I-Ging-Orakel.
Ansätze für 0-1-Systeme finden wir beim englischen Gelehrten Thomas Harriot (1560-1621) und seinem schottischen Kollegen John Napier (1550-1617). Der englische Politiker und Philosoph Francis Bacon (1561-1626) entwarf eine binäre Geheimschrift. Harriot hat seine mathematischen Ideen nie publiziert; Napiers Arithmetica localis wurde veröffentlicht, sie enthielt jedoch keine Schreibweise mit Stellenwerten. Zu jener Zeit hatten die Gebildeten im übrigen genug damit zu tun, das Rechnen mit den zehn Dezimalziffern zu erlernen.
Vor 350 Jahren erschien aber eine Darstellung der Dualzahlen in einem Buch. Der Verfasser hieß Juan Caramuel y Lobkowitz; er wurde am 23. Mai 1606 in Madrid geboren. Sein Vater war Militäringenieur und entstammte einer luxemburgischen Familie – der Großvater hieß Cramer. Die Mutter hatte dänische und böhmische Ahnen. Juan beherrschte als Kind die Grundlagen von Mathematik und Astronomie, Schule und Hochschule absolvierte er in Rekordzeit. Mit fünfzehn trat er als Doktor der Philosophie in den Zisterzienser-Orden ein. Mit zwanzig unterrichtete er das Fach.
Nun begann für ihn ein ruheloses Leben mit Stationen in Flandern, dem Deutschen Reich, Böhmen und Italien. Caramuel war Universalgelehrter, verstand zwei Dutzend Sprachen und produzierte Buch auf Buch. Daneben war er streitlustig und recht tolerant; mindestens eine Schrift von ihm kam auf den päpstlichen Index. Von 1657 bis 1673 bekleidete er den Bischofssitz von Campagna östlich von Salerno, danach leitete er das Bistum Vigevano in Norditalien. Beide Orte lagen im spanischen Einflussbereich. Caramuel starb in Vigevano am 8. September 1682.
In seiner Zeit in Campanien verfasste Caramuel ein Buch mit zwei Bänden und insgesamt 1711 Seiten. Es erschien 1670 unter dem Titel Mathesis biceps, vetus et nova. Das erste Wort stand für die mathematischen Wissenschaften, „biceps“ heißt zweiköpfig. Die alten Fächer („vetus“) waren für Caramuel Arithmetik, Algebra, Geometrie und Geodäsie; unter den neuen („nova“) verstand er logarithmisches Rechnen, Kombinatorik und Trigonometrie sowie die Mechanik und die Astronomie. Dazu kamen Spezialthemen wie beispielsweise mathematische Instrumente.
Den Arithmetik-Teil in Band I eröffnete Caramuel mit einem Vorwort. Es begann mit einem Philosophenzitat: „Neocli interroganti, Cur Homo, animal sapientissimum sit? respondit Plato, ΟΤΙ ´AΡΙΘΜΕΙΝ ΙΣΑΣΙ, quia numerare scit.“ Oder auf Deutsch: „Dem Neocles, als er fragte, warum der Mensch das weiseste Lebewesen sei, antwortete Plato, weil er zu zählen weiß.“ Falls der Spruch stimmt, fiel er in der ersten Hälfte des vierten Jahrhunderts v. Chr. Plato starb 348 oder 347 v. Chr.; Neocles hieß der Vater des griechischen Denkers Epikur, der 341 v. Chr. geboren wurde.
Der Mensch ist das Wesen, das zählt. Von dieser schönen Definition kam Caramuel durch philosophische Überlegungen zu der Tatsache, dass die Menschen ebenso die Zahlen erschufen. Die alten Römer taten es durch Einschlagen von Nägeln; so hielten sie die Dienstjahre ihrer Konsuln fest. Später erfanden sie die römischen Zahlen aus Buchstaben. Bei Angaben von mehr als einer Million gingen den Römern aber die Zahlzeichen aus. Zum Glück gab es für den „Vorzahlenmenschen“, wie Caramuel ihn nannte, eine Alternative.
Das war das Stellenwertsystem. Juan Caramuel führte es nicht auf die arabischen und indischen Zahlen, sondern auf die Logarithmen-Erfinder John Napier und Henry Briggs zurück. In seinem Vorwort stellte er mehrere Systeme vor. Das erste umfasste die Ziffern 0 und a, die bei Caramuel die 1 vertrat, wie unten erkennbar. Der dazugehörige Artikel De Binaria Arithmetica füllt mit vier Zahlenlisten und einer Anmerkung („Nota“) zweieinhalb Seiten. Er ist die älteste gedruckte Präsentation der Dualzahlen.
Unsere Liste zeigt die Folge 0, a, a0, aa, a00,… Caramuel sah, dass Zweierpotenzen – er sprach von Perioden und Umläufen – zunächst langsam anwachsen, dann aber schnell sehr groß werden: periodos haberet satis magnas. Ihm fiel außerdem auf, dass die Differenzen zwischen den Potenzen 1, 2, 4, 8,… wieder die gleiche Zahlenfolge ergeben. 2 minus 1 ist 1, 4 minus 2 ist 2, 8 minus 4 ist 4 und so weiter und so fort. Dagegen liefern die Differenzen bei den Zehnerpotenzen die Folge 9, 90, 900,…
Caramuel suchte nun Anwendungen des Dualsystems und fand sie in der Musik. Er wusste von den Beziehungen zwischen den Längen von Saiten und den Tönen, die beim Anzupfen entstehen. Wenn eine Saite einen bestimmten Ton erzeugt, dann erklingt die doppelt so lange Saite eine Oktave tiefer. Er rechnete dann in fünfzig Zweierschritten die Saitenlängen von 1 bis 1.125.899.906.842.624 aus. Neben jeder Zweierpotenz notierte er den Exponenten – er benutzte den Ausdruck Logarithmus – und neben der Liste Per quinquaginta Octavas descendentes. Das heißt übersetzt: durch fünfzig Oktaven absteigend.
Nach dem Dualsystem schaute sich Caramuel Systeme mit den Grundzahlen 3 bis 10 sowie 12 und 60 an. Sein Fazit lautete, dass alle Arithmetiken analog sind – siehe den Vermerk unten links. Der erwähnte Thomas Harriot tat noch mehr. In seinem Nachlass fand sich ein Blatt mit dualen Additionen, Subtraktionen und Multiplikationen. Gottfried Wilhelm Leibniz erläuterte binäre Operationen in der Explication de l’arithmétique binaire. Sie erschien 1703 in Paris. Ungedruckt blieb sein Manuskript De progressione dyadica von 1679. Es skizzierte unter anderem ein binäres Rechengerät.

Für den Dom von Vigevano entwarf Caramuel eine konkav gerundete Fassade. So bemerkt kaum jemand, dass die Kirche schräg zur davor gelegenen Piazza steht. (Foto Magagnini Carlo Alberto CC BY-SA 4.0 am Rand beschnitten).
Seit dem Artikel von 1703 galt Leibniz als der Vater des Dualsystems. Caramuels Leistung geriet nach und nach in Vergessenheit. Leibniz wusste von der „Mathesis biceps“; dass sie ihn zum binären Zahlensystem führte, ist aber nicht anzunehmen. Es handelt sich wohl um eine Parallelerfindung. Auf Deutsch wurde das Dualsystem zuerst 1775 gelehrt: hier geht es zu der Schrift des berühmten Feinmechanikers Georg Friedrich Brander. Wer noch mehr über Leben und Werk von Juan Caramuel y Lobkowitz erfahren will, kann dieses Buch abrufen.
Wir bedanken uns sehr herzlich bei der Fachschaft Latein des Gymnasiums Theodorianum und Frau Berit Dammaschke für die Hilfe bei der Übersetzung des lateinischen Textes.



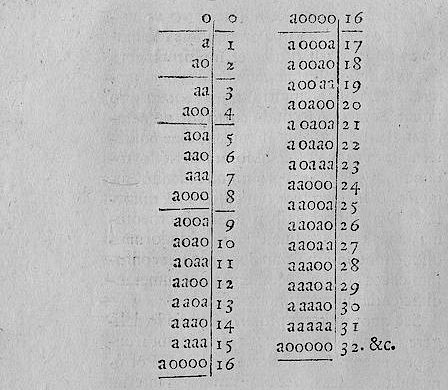
Danke für den schönen Beitrag! Der Engel auf dem Titelblatt mag aber wohl eher die Logarithmentafel (mit Logarithmen zur Basis 2) als die Zweierpotenzen. Das Spruchband „Metitur Terram, Mare, Ventos, Astra Mathesis; Antiqua immenso tempore, nostra brevi“ spielt vermutlich auf die Logarithmen an, die die mathematischen Methoden zur Vermessung der Welt enorm beschleunigt haben. Die Vermessung des Kosmos ist neben der Logarithmentafel ikonenhaft dargestellt.
Noch ein Kuriosum zum Dualsystem: 1813 veröffentlichte Karl Drais, der Erfinder der Draisine und des Laufrads, im Badischen Magazin eine kurze Vorankündigung eines geplanten Buches mit dem Titel „Dyadik“. Darin rechtfertigt er sein zukünftiges Buch so: „Das dyadische Rechensystem wurde schon vor mehr als hundert Jahren von dem großen Leibnitz aufgestellt, ist aber bis zur Stunde noch nicht genug gewürdigt worden.
In der Aufstellung eines ganzen dyadischen Systems hingegen bin ich […] der erste.“
Das Buch erschien tatsächlich im folgenden Jahr. Es hatte 16 Seiten und sollte dem misslichen Umstand, dass „der grosse Leibnitz leider zu früh gestorben ist, um die Welt von dieser Wahrheit zu überzeugen“, abhelfen.
Drais hoffte, dass ein einsichtsvoller Regent das dyadische System für die Staatsgeschäftsgänge einführen würde; die Staatsdiener würden es in wenigen Tagen erlernen. Zweierpotenzen gäbe es schließlich überall: „Wie angenehm ist es nicht, wo es so üblich ist, dass eine Maas gerade 2 Bouteillen 4 Schoppen und 8 Gläser, ein Malter 8 Simmern, ein Simmern 16 Mäßel, ein Pfund 32 Loth, ein Loth 4 Quintchen, ein Conventionsthaler 2 schwere Gulden, ein Batzen 4 Kreuzer, ein Kreuzer 4 Pfennig, eine Carolin 4 grosse Thaler, eine Ducat 2 Kronenthaler, ein Sechsbätzner 2 Dreybätzner, ein Dreybätzner 2 Sechser und ein Sechser 2 Groschen hat.“
Leibniz selbst hingegen war von der Praktikabilität des Dualsystems gar nicht überzeugt, denn er schrieb: „Cependant je ne recommande point cette manière de compter, pour la faire introduire à la place de la pratique ordinaire par dix. […] La pratique par dix est plus abrégée, & les nombres y sont moins longs“.
Das Badische Magazin von 1813 findet man hier:
https://books.google.ch/books?id=FGxEAAAAcAAJ
Die Schrift „Dyadik“ von Drais hier:
http://mdz-nbn-resolving.de/urn:nbn:de:bvb:12-bsb10729250-2
Und das Zitat von Leibniz hier:
https://hal.archives-ouvertes.fr/file/index/docid/104781/filename/p85_89_vol3483m.pdf