Rechnen durch Hingucken

In einer Multiplikationstafel lässt sich das Produkt von zwei Zahlen einfach nachschlagen. Die Rechentafeln mit Zahlen führten zu graphischen Tafeln. Hier wird das Resultat an Kurven oder geraden Linie abgelesen. Im 19. Jahrhundert erfand der französische Ingenieur Philbert Maurice d’Ocagne die Nomographie. Sie erweiterte das graphische Rechnen beträchtlich. Ihre Genauigkeit entspricht etwa der des Rechenstabs.

Zu den ältesten Rechenhilfen gehören die mathematischen Tabellen. Sie listen einfach bereits ausgerechnete Resultate auf. Schon die alten Babylonier kannten Multiplikationstafeln, die zu zwei Zahlen das Produkt nannten. Später kamen solche für Sinus und Cosinus hinzu und natürlich die Logarithmentafeln. Diese wurden noch vor 50 Jahren in der Schule gelehrt.

Am Ende des 18.Jahrhundert entdeckte der Franzose Louis-Ézéchiel Pouchet, dass sich die Ergebnisse einer Multiplikation auch graphisch darstellen lassen. Man legt dazu ein Koordinatensystem mit zwei Achsen an und verbindet gleiche Produktwerte durch eine Kurve. Das Bild unten zeigt die Lösung der Aufgabe 4,8 x 5,1. Das Resultat 24,48 wird als 24,5 aus der Zeichnung abgelesen. Der Verlust der Genauigkeit ähnelt den Abschätzungen, die der Benutzer eines Rechenstabs vornimmt.

Multipliziertafel von Louis-Ézéchiel Pouchet

Statt eines normalen Koordinatengitters kann man eines mit logarithmischer Teilung verwenden. Hier liegen gleiche Produkte von x und y auf einer Geraden, was das Ablesen beträchtlich erleichtert. Im 19. und im 20. Jahrhundert entstanden in Frankreich und Deutschland entsprechende Druckwerke. Mit ihrer Hilfe wurde nicht nur graphisch multipliziert und dividiert, sondern auch die Wurzel gezogen. Ein schönes Beispiel ist das Rechendiagramm von Strantz, das 1947 in Hannover erschien. Leider hat sich kein Exemplar des Werks in größeren Bibliotheken erhalten.

Einen anderen Weg ging in den 1880er-Jahren der französische Ingenieur Philbert Maurice d’Ocagne. Er nahm das rechtwinklige Koordinatensystem auseinander und setzte die Achsen parallel aufs Papier. Zwischen die Achsen legte er eine weitere Linie, die gerade oder gebogen sein kann. Man stelle sich nun zwei Punkte A und B auf den Achsen vor. Wenn man sie durch eine Gerade verbindet, erhält man einen oder mehrere Schnittpunkte mit der Linie in der Mitte oder aber gar keinen Schnittpunkt.

Die Achsen und die Kurve dazwischen lassen sich mit einer Skaleneinteilung versehen. Die Wahl der Nullpunkte ist frei, die Skalen können gleichmäßig unterteilt sein oder auch unterschiedliche Dichte aufweisen. Auf jeden Fall erhält jeder Punkt auf den Linien einen Zahlenwert. Mit einer solchen Graphik, Nomogramm genannt, können wir mathematische Aufgaben lösen. Die Eingaben sind die Werte der Punkte auf den Achsen. Ausgegeben wird die Zahl oder die Zahlengruppe für den Schnittpunkt bzw. die Schnittpunkte dazwischen.

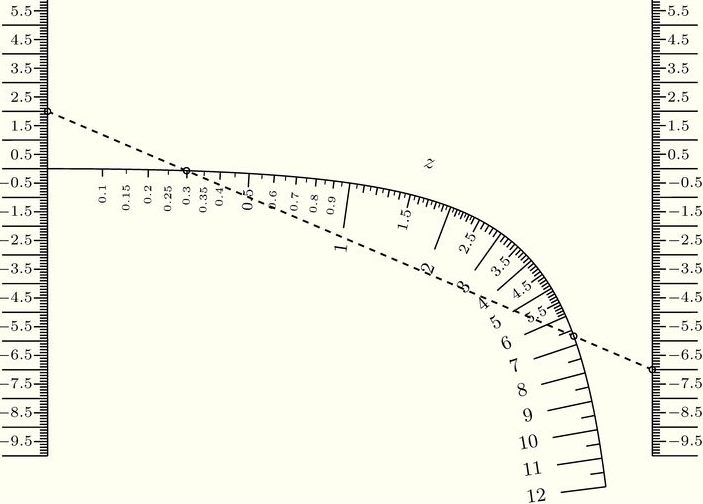
Nomogramm für die Nullstellen einer quadratischen Gleichung  (CC BY-NC-ND 3.0)

Eine Anwendung zeigt obiges Bild. Gesucht werden die Nullstellen einer Gleichung z² + p z + q = 0. Die Zahlen p und q sind an den Skalen links und rechts eingestellt, es heißt also z² – 7 z + 2 = 0. Als Nullstellen erhalten wir 0,3 und 6,7. Das sind die Zahlenwerte der Schnittpunkte zwischen der gestrichelten Verbindungslinie und der mittleren Skala. Die Genauigkeit beträgt nur eine Kommastelle. Wer in der Schule aufpasste und die Formel für Nullstellen weiß, kommt sicher zu besseren Werten.

Das zweite Beispiel findet sich im Eingangsbild zum Blog. Es ist die Berechnung des Body-Mass-Index, des Quotienten aus Körpergewicht und quadrierter Körperlänge. Die linke Skala drückt die Größe in Fuß und Metern aus, die rechte erfasst die Masse in US-Pfund und Kilo. Die Aufgaben verdeutlichen eine Grundregel der Nomographie: Ein Nomogramm gilt in der Regel nur für einen beschränkten Wertebereich. Eine Body-Mass-Index für Kinder erfordert eine neue Graphik. Analog verhält es sich für größere oder kleinere Parameter der quadratischen Gleichung.

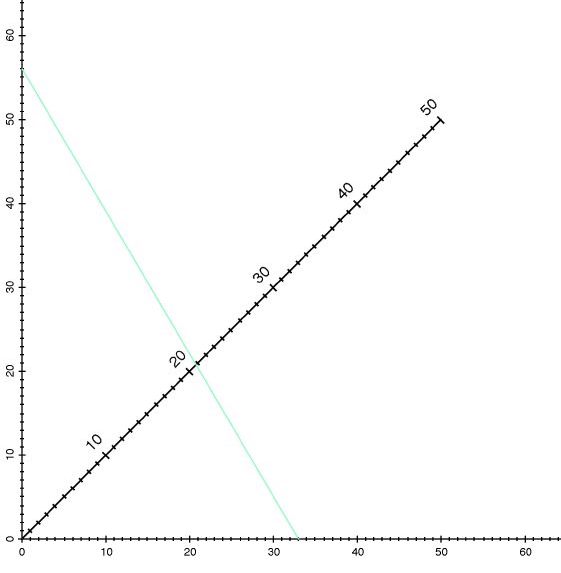
Die Fachliteratur hält noch andere Typen von Nomogrammen bereit, etwa das im Bild unten. Es verkörpert die Formel 1/x + 1/y =1/z, die in der Elektrotechnik eine Rolle spielt. An den äußeren Skalen werden x = 33 und y = 56 eingestellt. Der Schnittpunkt der schrägen Skala mit der blauen Linie liefert die Ausgabe z = 20,8. Wer noch mehr zur Nomographie erfahren möchte, findet es in diesem Blog und einer Einführung. Eine Geschichte der Technik steht hier, und hier geht es zu einem Rechengerät.

Zeichnung: Daniel P. B. Smith, CC BY-SA 3.0

Eingangsbild: CC BY-NC-ND 3.0